
Fogalma, rövid leírása
A henger fogalmát úgy érthetjük meg, ha letisztázzuk, hogy a hengert hogyan kell származtatni. Vegyünk a síkon egy tetszőleges zárt síkidomot. Döfjük át a síkot egy egyenessel. Ezzel az egyenessel húzzunk párhuzamost minden pontján keresztül a zárt síkidomnak. Így kapunk egy végtelenbe nyúló hengerfelületet. Ha ezt a hengerfelületet elmetsszük egy, az eredeti síkkal párhuzamos síkkal, akkor egy zárt hengerteret kapunk.
Alapvetően tévhit, hogy egy henger vagy egyenes hasáb lehet, vagy hogy kör alapú. Léteznek például ellipszis alakú hengerek is.
Amennyiben a síkon felvett síkidom zárt sokszög, akkor hengerszerű hasábról beszélhetünk.
Amennyiben a döfő egyenes merőleges a síkra, akkor egyenes hasábról beszélünk.
Amennyiben a síkon felvett síkidom kör, akkor a létrejövő henger körhenger.
Amennyiben a síkon felvett síkidom kör és a döfő egyenes merőleges a döfött síkra, akkor egyenes körhengerről beszélünk (a matematika órán mindig ezt értettük henger alatt, de ez valójában egy egyenes körhenger). A továbbiakban erről lesz szó.
A henger térfogata
Ahhoz, hogy a henger (egyenes körhenger) térfogatát meg tudjuk határozni, először definiálnunk kell a henger egyes részeit. A henger két határoló körét a henger alapjának és fedőlapjának nevezzük. Az egymással párhuzamos egyenesek által meghatározott felületet pedig alkotónak nevezzük. Szemléljük az alábbi ábrát!

A hengerszerű test magassága a párhuzamos síkok távolsága. Egy egyenes körhenger esetén ez megegyezik az alkotók hosszával.
A körhenger sugarát jelöljük r-el. Ekkor a henger (körhenger) térfogata a következő képlettel számítható ki:

Ez nem más, mint a henger alapkörének területének és a magasságának a szorzata.
A henger felszíne
A henger (egyenes körhenger) felszíne úgy számítható ki, hogy az alapkör és a fedőkör területét összeadjuk a palást felszínével.
Az alapkör és a fedőkör egybevágó körök, területük a kör területszámításával számítható ki. A henger palástjának területe egyenlő a kiterített téglalap területével, melynek oldalhosszai a henger magassága és az alapkör kerülete. Így a henger felszíne az alábbi módon számítható ki:
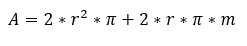
Állítások az egyenes körhengerrel kapcsolatban
Minden körhengernek ugyanakkora a térfogata, melynek a magassága azonos hosszúságú és az alapkörei egybevágóak. Tehát, az alábbi két körhenger térfogata egyenlő.

- Ha egy egyenes körhengert elmetszünk egy, az alapkörökre merőleges síkkal, akkor a síkmetszet mindig téglalap lesz.
- Adott térfogat mellett a henger felszíne h=2r esetben minimális.
- Adott felszín mellett a térfogat h=2r esetben maximális.
Hol jelenik meg ez a test a való életben?
A henger forma számos esetben megfigyelhető a környezetünkben. Néhány példa rá:
- Egy tolltartó alakja
- A konzervdoboz alakja
- Pohár formája
- Alufólia tartó hengere
- A fazék formája (mennyi levest főztünk meg?)
Habár a legtöbb embernek nem szükséges az érettségi vizsga után a hengerrel kapcsolatos képletek és állítások a mindennapjaihoz, azonban a való életben illik tudni, hogy mit jelent a hétköznapokban a „henger forma”.
Összefoglalás
A henger már az ötödik osztályos matematika számonkéréskor is előkerül. Mégis miért fontos, hogy tisztában legyünk a hengerre vonatkozó legfontosabb állításokkal és összefüggésekkel? Azért, mert a középiskolai felvételin, és az érettségin is rendszeresen jönnek elő olyan kérdések, melyek a hengerhez kapcsolódnak.



