VAGY

A deltoid fogalma
A deltoid egy olyan tengelyesen szimmetrikus négyszög, melynek az egyik átlója a szimmetriatengelye és 2-2 szomszédos oldala azonos hosszúságú.
Tulajdonságai
- Két-két szomszédos oldala azonos hosszúságú
- Átlói merőlegesek egymásra
- A szemmetria átlója felezi a másik átlót egyenesét
- A különböző hosszúságú oldalai által bezárt szögek egyenlőek
A deltoid kerülete
A deltoid kerületét ugyanúgy számolhatjuk ki, mint bármely négyszögét: a négy határoló oldal hosszának összegét vesszük. Mivel 2-2 szomszédos oldala egyenlő, ezért az alábbi megállapítás tehető:
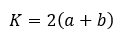
ahol a és b a deltoid két oldalhosszát jelöli.
A deltoid területe
Felmerülhet bennünk a teljes jogos kérdés: különbözik-e a deltoid területszámítása abban az esetben, ha konvex, illetve konkáv négyszögről beszélünk? A válasz az, hogy nem. Minden esetben az alábbi képlet használható, ahol e és f jelöli a deltoid átlóinak hosszát.

Ennek meggondolása roppant egyszerű. Először nézzük meg a konvex deltoid esetét!

Ahogy az ábra is mutatja, könnyedén kiegészíthető a négyszög egy téglalappá. Ennek a területének pont a felével egyenlő a deltoid területe, a megfelelő egybevágó háromszögek terület-egyenlősége miatt.
Amennyiben konkáv a deltoid, abban az esetben is igaz az állítás. Szemléljük az alábbi ábrát!

A teljes téglalap területére az alábbi összefüggés írható fel:
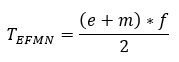
Ahhoz, hogy a deltoid területét meghatározzuk, ki kell vonni az EMG, GNF, EHO, HOF háromszögek területét. Ezek közül 2-2 háromszög egybevágó, így az egyenletet felírva

A deltoid területét kiszámíthatjuk úgy is, hogy a két oldalát és a közbezárt szögük szinuszát összeszorozzuk. Ez képletszerűen így néz ki:
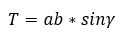
Mit érdemes tudni egy konvex és konkáv deltoidról?
A konvex deltoid minden belső szöge kisebb, mint 180 fok. Egy konkáv deltoid valamely szöge nagyobb, mint 180 fok. Az alábbi ábra 1-1 deltoidot szemléltet. Az első egy konvex deltoid, a másik egy konkáv deltoid.

Igaz állítások erre a négyszögre vonatkozóan
- Minden deltoid, mely konvex, egyben érintőnégyszög is. Tehát, minden deltoidnak, amely konvex, van beírt köre.
- Minden deltoid, melynek az oldalai egyenlőek, egyben rombusz is.
- Minden deltoid tengelyesen szimmetrikus négyszög.



