VAGY


Fogalma
Ahhoz, hogy a húrtrapéz fogalmát megismerhessük, érdemes először a trapézt definiálni. A trapéz egy olyan négyszög, melynek van párhuzamos oldalpárja. Ezek után definiáljuk a húrtrapézt is! A húrtrapéz egy olyan trapéz, melynek van körülírt köre.
Tulajdonságai
A húrtrapéz tulajdonságai a négyszögek és a trapéz tulajdonságain túl:
- Tengelyesen szimmetrikus négyszögek
- Van körülírt körük
- Szárai egyenlő hosszúak
- Átlói egyenlő hosszúak
A húrtrapéz területe
A húrtrapéz területét pontosan úgy kell kiszámolni, mint a trapézok területét. Lássuk az alábbi képletet!
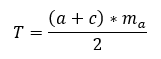
ahol a és c az alapokat jelölik, míg m_a a húrtrapéz magasságát.
A húrtrapéz kerülete
A húrtrapéz kerületét pontosan ugyanúgy kell kiszámolni, mint a trapézét, vagy mint bármely négyszögét. Csak össze kell adnunk az oldalai hosszát.
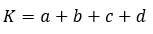
Amennyiben az alapok hosszát a és b jelöli, a szárak hosszát c és d, kijelenthető, hogy c = d. Ez esetben a képet az alábbira módosul:
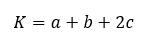
A húrtrapéz szerkesztése
Az alábbi ábra egy lehetséges szerkesztését mutatja be a húrtrapéznak. Először vegyünk fel a síkon egy tetszőleges kört, és annak egy húrját, mely jelen esetben a BC szakasz. Ez után jelöljünk ki egy D pontot a kör kerületén, és ezt kössük össze a közelebbi végpontjával a BC szakasznak. A D ponton keresztül húzzunk párhuzamost a BC szakasszal, így kapjuk a négyszög utolsó pontját, az E pontot.

Összefoglalás
A húrtrapéz mindig is esszenciális részét képezte az iskolai, általános iskolás tananyagnak. Már a gimnáziumi felvételin is elvárás, hogy a diákok tisztában legyenek a húrtrapézokat értintő elemi állításokkal. Annál is inkább fontos témakör, hiszen a matematika érettségin is rendszeresen megjelenő téma.



