Fogalma, rövid bemutatása
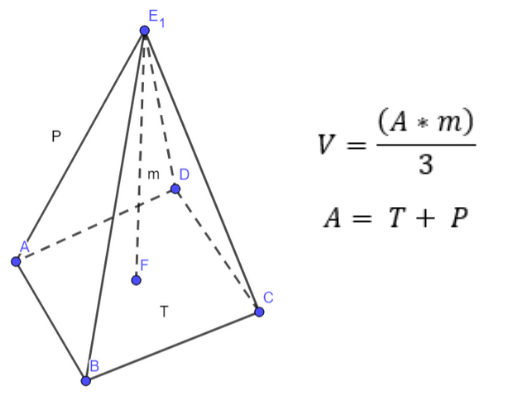
A gúla egy olyan geometriai test, melynek alapja egy n-oldalú sokszög, palástja pedig n darab háromszögből áll. A palástháromszögek egyik csúcsa egy olyan pontban találkoznak, mely nem esik egy síkba az alappal.
A gúla elnevezése roppant egyszerű: aszerint kell eljárnunk, hogy az alapot alkotó sokszög micsoda. Például ötszög alapú gúla, hatszög alapú gúla.
Egy gúla akkor szabályos, ha az alaplapja szabályos sokszög, és az alaplapon nem található csúcsának az alaplapra merőleges vetülete az alap középpontjában van.
Lapjainak, éleinek és csúcsainak száma.
Amennyiben egy gúla alapjának oldalainak száma n, akkor a lapjainak és csúcsainak száma egyaránt n+1, ahol n az alap oldalainak száma. A gúla éleinek száma ekkor 2n.
A gúla térfogata
Amennyiben egy gúla alapterületét T-vel jelöljük, magasságát pedig m-el, akkor a gúla térfogata

Ez a képlet ismert lehet a tetraéder térfogatszámításából. Ez természetesen így van, hiszen a tetraéder is gúla, tulajdonképpen egy olyan gúla, melynek alapja egy háromszög.
A gúla felszíne
Egy gúla felszínét pontosan úgy kell kiszámolni, mint bármely poliéderét. Adjuk össze a testet határoló lapok területének az összegét, és megkapjuk a test felszínét. A felszín számításkor az alap és palást területére szoktuk a gúla felszínét bontani, tehát
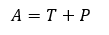
Abban az esetben, ha a gúlába gömb írható, fennáll az alábbi összefüggés, ahol r a beírt kör sugara, V pedig a gúla térfogata, A pedig annak felszíne.
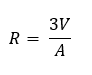
Speciális esetei
- Az egyenes gúla egy olyan gúla, ahol az alapon nem fekvő csúcspont az alap szimmetriaközéppontja felett helyezkedik el.
- A szabályos gúla egy olyan egyenes gúla, amelynek az alapja szabályos sokszög. A szabályos tetraéderek és a mindenki által ismert négyzet alapú piramisforma is szabályos gúla.
- A tetraéderek a háromszög alapú gúlák.
Érdekességek
- A gúlákkal rokon testek a bipiramisok, mely két, alapjuknál összeillesztett gúlából tevődik össze.
- A tetraéderek között az adott felszínhez tartozó maximális térfogatú test a szabályos tetraéder.
- Bármely kocka három egybevágó négyzet alapú gúlára osztható, amiknek csúcsai a kocka csúcsaiban találkoznak.
Összefoglalás
A gúla térfogata és felszíne már általános iskolában is tananyag – a gimnáziumi felvételin rendszeresen jelennek meg olyan feladatok, melyek a gúlával kapcsolatosak. Az érettségin is rengetegszer vannak gúlával kapcsolatos számítások. Hogyan számítható ki a gúla térfogata és felszíne? Mik a gúla részei? Mi az a csonka gúla, vagy négyzet alapú gúla? Ezekkel a kérdésekkel érdemes tisztában lennünk.



