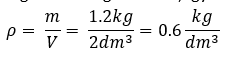A sűrűség fogalma már általános iskolában is előkerül a fizika órákon. Habár, életünk során már korábban is találkozunk a sűrűséggel még akkor is, ha nem ismertük a pontos fogalmát. Gondoljunk csak arra, amikor két különböző labda közül, melyeknek a térfogata nagyjából egyenlő volt, az egyik jóval nehezebb volt. De lehet, hogy láttunk példát arra is, hogy két fémdarab közül a méretbeli egyezőség ellenére az egyik jóval könnyebb volt – az, amelyik alumíniumból készült. Mi a sűrűség jele, képlete? Hogyan számítjuk ki? Cikkünkben ezekre a kérdésekre keressük a választ.
A sűrűség fogalma
Végezzünk kísérletet. Vegyünk különböző méretű fémdarabokat, melyek ugyanabból az ötvözetből készültek. Mérjük meg ezeknek a daraboknak a tömegét és a térfogatát egyenként, és az eredményeket foglaljuk táblázatba. A tömeg méréséhez nyugodtan használjunk mérleget. A térfogat méréséhez pedig használjunk egy mérőpoharat, melyet megtöltünk vízzel – a térfogatot mérjük meg a víz kiszorításának módszerével. Az alábbi táblázat különböző vasdarabok tömegét és térfogatát ábrázolja.

Ábrázoljuk a kapott eredményeket egy derékszögű koordináta-rendszerben. Ha megfigyeljük, akkor láthatjuk, hogy a kapott pontok egy egyenesre illeszkednek. Ebből következik az, hogy a testek térfogata és tömege között egyenes arányosság lelhető fel.

Ha a táblázatban levő értékek hányadosát vesszük, akkor a tömeg és térfogat hányadosára egy állandó, konstans értéket kapunk. Ez a meghatározott konstans a méret vasötvözet sűrűsége.
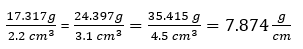
Amennyiben homogén anyagról beszélünk, az alábbi összefüggés mindig igaz lesz, hiszen egy adott test tömegének és térfogatának hányadosa állandó.
Egy test tömegének és a térfogatának hányadosa az anyag jellemzője, az így meghatározott fizikai mennyiséget sűrűségnek nevezzük. A sűrűség jele (görög Rhó betű). Képlet szerűen a sűrűség kiszámítása:
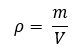
A sűrűség SI mértékegysége:
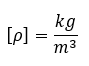
Szintén használatos még a g/cm^3 is.
Az átlagsűrűség fogalma
Könnyen előfordulhat, hogy egy testnek a sűrűsége nem homogén. Ez nem feltétlenül csupán a test anyagának egyenletlenségeire vezethető vissza, hanem akár arra is, hogy a testet több darabból állították össze. Remek példa lehet erre egy kézi balta, melynek a feje és a nyele teljesen más anyagból készül. Ez esetben a test átlagsűrűségét érdemes megadni. Egy test átlagsűrűsége nem más, mint a teljes tömegének és teljes térfogatának a hányadosa.
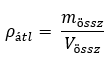
Néhány fontos anyag sűrűsége táblázatban foglalva
Na jó – eddig beszélünk rengeteg mindenről, ami csupán elmélet. De felmerül bennünk a teljesen jogos kérdés, hogy mégis mekkora sűrűség értéke van a különféle anyagoknak számszerűsítve? Nos, íme egy összefoglaló táblázat, amely rengeteg anyagféle sűrűségét magában foglalja.

Ismétlő kérdések, gyakorló feladatok
Íme, néhány gyakorló példa, melyen tesztelheted a tudásodat.
I. Feladat
Mi a sűrűség mértékegysége? Válasszuk ki a helyes opciót!
A,
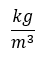
B,
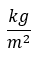
C,
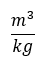
Megoldás.
A helyes megoldás az (A). A sűrűség mértékegysége kg/m^3.
II. Feladat
A homogén anyagból készült testek tömege és térfogata között
A,
egyenes arányosság lelhető fel.
B,
fordított arányosság lelhető fel.
C,
négyzetes arányosság lelhető fel.
Megoldás.
A helyes válasz az (A). A homogén anyagból készült testek tömege és térfogata között egyenes arányosság lelhető fel.
III. Feladat
Egy tégladarab térfogata 2 d, míg tömege a mérlegre helyezve 1.2kg. Határozzuk meg a sűrűségét!
Megoldás.
Használjuk a sűrűség képletét! A tömeg és a térfogat ismert, így a helyes számítás: