VAGY
A paralelogramma fogalma
A paralelogramma egy olyan négyszög, melynek van 2-2 párhuzamos oldalpárja.
A négyszög tulajdonságai
A paralelogrammáról számos érdekes tulajdonság fogalmazható meg. Lássunk ezek közül párat!
- Szemközti oldalai egyenlő hosszúak
- Szemközti oldalai párhuzamosak
- Átlói felezik egymást
- Szemközti szögei egyenlő nagyságúak
- Középpontosan szimmetrikus alakzat
- Az egy oldalon fekvő szögei 180 fokra egészítik ki egymást
- A két szemközti oldalának felezőpontját összekötő középvonal párhuzamos és egyenlő a másik két oldallal
- szimmetriaközéppontja az átlók metszéspontja.
Szokásos jelölései
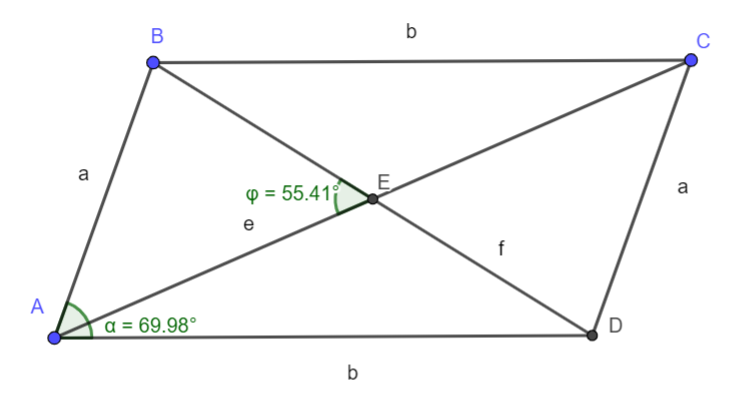
A paralelogramma
- oldalai rendszerint a és b-vel jelöltek
- átlói rendszerint e és f-el jelöltek
- magasságait az oldalaknak megfelelően és jelöli
Íme, egy ábra, mely szemlélteti mindezt.

A paralelogramma területe
Természetesen ennek a négyszögnek is sokféle módon lehet kiszámítani a területét és a kerületét. Lássunk ezek közül egy párat!
A paralelogramma területe megkapható az alap és a magasság szorzataként. A korábbi jelöléseket használva

A paralelogramma területét meghatározhatjuk úgy is, hogy összeszorozzuk két oldalát, és a közbezárt szög szinuszát.
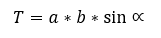
A paralelogramma területének egy szintén lehetséges meghatározási módja, hogy összeszorozzuk az átlóit és az általuk közre zárt szög szinuszát.
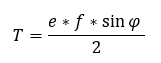
A paralelogramma kerülete
A paralelogramma kerülete ugyanúgy határozható meg mint ahogy minden egyes négyszögé: össze kell adni az oldalait. Jelen esetben kijelenthető, hogy a szemközti oldalai ugyanolyan hosszúak, így a helyes összefüggés az eddigi jelölésekkel az alábbi:
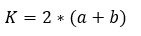
A négyszög speciális esetei
Természetesen ennek a négyszögnek is vannak speciális esetei. Lássuk, hogy mik ezek!
- Ha egy paralelogramma minden oldala egyenlő, akkor rombusz is egyben.
- Ha egy paralelogramma szögei derékszögek, akkor téglalap is egyben.
- Ha egy paralelogramma szögei és oldalai is egyenlőek, akkor négyzet is egyben.
Érdekességek
- Matematikailag bizonyított tény, hogy bármely sík lefedhető egy adott paralelogrammával akár többféle képpen is.
- A paralelepipedon egy olyan speciális test, melynek minden egyes oldala paralelogrammákból tevődik össze.
- Már az ókorban is ismerték a fogalmát, az Euklideszi geometria egyik definiált síkidoma volt.
Próba feladatok
Íme, néhány próba feladat, amin érdemes lehet letesztelni a paralelogrammákkal kapcsolatos tudásunkat. Ezen feladatok természetesen nem csupán a cikkünkben írt tényeket és állításokat érintik, hanem az általános matematikai tudásunkat is.
I. feladat
Döntsük el az alábbi állításokról, hogy igazak-e vagy hamisak!
A,
A paralelogramma átlója szögfelező is.
B,
Ha egy négyszög két átlója egyenlő hosszú, akkor az a négyszög paralelogramma.
C,
Minden paralelogramma trapéz, de nem minden paralelogramma rombusz.
Megoldás.
Az A, állítás hamis. Amennyiben a paralelogramma két szomszédos oldala nem egyenlő, akkor az átlója nem szögfelező. A B, állítás is hamis, csak és kizárólag abban az esetben igaz, ha felezik egymást az átlók. A C, állítás igaz, hiszen a paralelogrammának mindig van párhuzamos oldalpárja, azonban nem minden paralelogrammának egyenlőek az oldalai.
II. feladat
Egy paralelogramma átlóinak hossza 20 és 30 cm, bezárt szögük pedig 30 fok. Mennyi a területe?
Megoldás. Használjuk a jól ismert területszámító képletet! Amely szerint behelyettesítés után a végeredmény, a paralelogramma területe:

III. feladat
Egy paralelogramma oldalainak hossza rendre 10,20,30,20 egység. Számoljuk ki a kerületét!
Megoldás. Ez a feladat eleve hibás, hiszen nincs 2-2 egyenlő oldalpárja a négyszögnek. Ebből kifolyólag, és ennek köszönhetően a feladat értelmetlen.
Összefoglalás
A paralelogramma az egyik legfontosabb négyszög az elemei geometriában. Az érettségi, valamint felvételi vizsgákon rendszeresen találkozni fogunk olyan feladatokkal, melyek ehhez a négyszöghöz kapcsolódnak. Rengeteg embernek a napi munkája során is nagy szerepet játszik a geometriában megszerzett ismerete, például mérnököknek fontos lehet ez a fajta tudás.



