A térfogat (V) azt adja meg, hogy egy adott test mekkora helyet foglal el a térben. A térfogat SI mértékegysége a köbméter (m^3). A térfogatot (amennyiben edények térfogatáról van szó) űrtartalomnak nevezzük. A síkidomok és egyenesek térfogata nulla.
A kocka térfogata
Jelöljük a kocka oldalélének hosszát a-val. Ekkor a kocka térfogata az alábbi képlettel írható fel:

KOCKA TÉRFOGATSZÁMÍTÓ KALKULÁTOR - KATTINTS!
A téglatest térfogata
A téglatest térfogata a három élének szorzata. Ha a téglatest éleinek hossza rendre a, b és c akkor a térfogat képlete az alábbi:
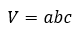
TÉGLATEST TÉRFOGATSZÁMÍTÓ KALKULÁTOR - KATTINTS!
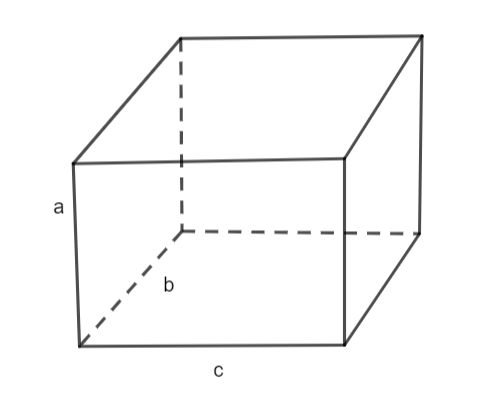
A henger térfogata
A henger (egyenes körhenger) térfogata úgy számítható ki, hogy az alapkör területét összeszorozzuk a magassággal. Ha az alapkör sugara r és a magasság m, akkor a helyes képlet:

Amennyiben a henger alapja nem kör, akkor a képlet a henger magasságának és a síkidom alapterületének szorzata.

HENGER TÉRFOGATSZÁMÍTÓ KALKULÁTOR - KATTINTS!
A gúla térfogata
A gúla térfogata az egyik háromszög alapterületének, valamint a hozzá tartozó magasság szorzatának harmada. Ez még abban az esetben is igaz, ha semmilyen speciális tulajdonsága nincs a gúlának. Ismétlésképpen: a gúla egy olyan test, melynek alaplapja egy n oldalú sokszög, palástja pedig olyan háromszögekből áll, melyek egy csúcsban találkoznak. Képlettel kifejezve:

ahol az alapterületet jelöli, míg az alapterülethez tartozó magasságot.

GÚLA TÉRFOGATSZÁMÍTÓ KALKULÁTOR - KATTINTS!
A tetraéder térfogata
A tetraéder egy olyan poliéder, melyet négy háromszöglap határol. Mivel mindegyik tetraéder gúla is egyben, ezért a térfogatszámítási képlet a következő lesz:

ahol az egyik háromszög alapterülete, pedig a hozzá tartozó magasság.
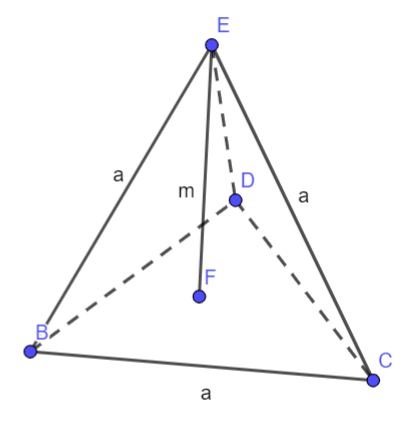
A négyzetes gúla térfogata
A négyzetes gúla egy olyan gúla, melynek alap síkidomja egy négyzet. A gúlák térfogatát az alábbi képlettel számíthatjuk ki:

ahol az alapterületet jelöli, míg az alapterülethez tartozó magasságot. Jelen esetben az alapterület egy négyzet, tehát a képlet az alábbi módon írható fel:
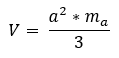
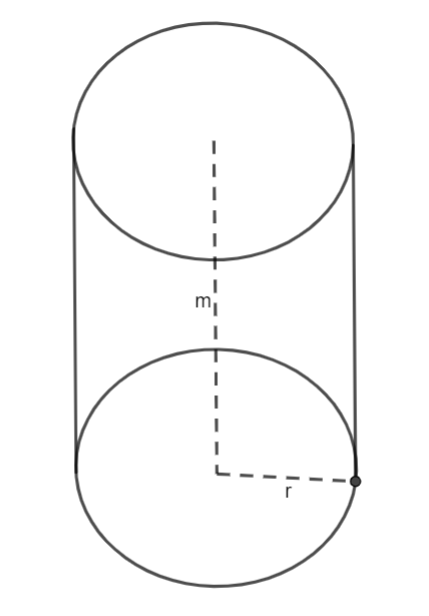
A kúp térfogata
Jelöljük a kúp alapkörének sugarát r-el, és a magasságát m-el. Ekkor az alábbi képletet használhatjuk:

A gömb térfogata
A gömb térfogatszámító képlete annak sugarának függvényében:

GÖMB TÉRFOGATSZÁMÍTÓ KALKULÁTOR - KATTINTS!
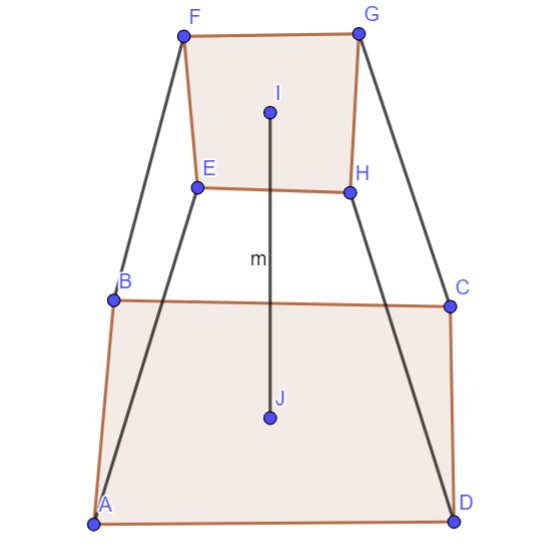
A csonka gúla térfogata
A csonkagúla térfogata annak magassága, valamint az alapterületek segítségével számítható ki. Jelöljük a magasságot m-el, a nagyobb területet T-vel, a kisebb területet t-vel. Ekkor a térfogat az alábbi módon számítható ki:

A csonka kúp térfogata
Jelöljük a csonka kúp nagyobbik határoló körének sugarát R-el, a kisebbik határoló körének sugarát r-el, a magasságot m-el. Ekkor a térfogatszámítás képlete az alábbi lesz:
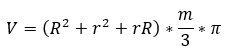
Hogyan számítható ki komplex testek térfogata?
Komplex testek esetén számolni nem egyszerű feladat. Általában modellező programokat használnak erre a célra. Egy lehetséges megoldás például az Inventor használata. Egy másik lehetséges megoldás – amennyiben meg tudjuk alkotni a testet kézileg – hogy a darabjait egy adott, meghatározott térfogatú edénybe helyezzük, és megmérjük a kiszorított víz térfogatát.
Összefoglalás
A térfogatszámítás rendszeresen előjön az érettségi vizsgákon - a hétköznapi életben gyakran kevezik a fogalmat az űrtartalom számítás fogalmával. Még a gimnáziumi felvételin is gyakran jönnek elő olyan feladatok, ahol meg kell határozni, hogy mekkora egy adott testekből álló alakzat térfogata. Ehhez pedig tudni kell, hogy hogyan kell meghatározni a térfogatát az egyes testeknek.
A való életben is megjelenik a térfogatszámítás. Például, ha meg szeretnénk becsülni, hogy egy vendégség alkalmával meddig kell megtölteni a teafőzőt, hogy elegendő teát főzzünk mindenki számára.



