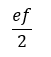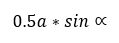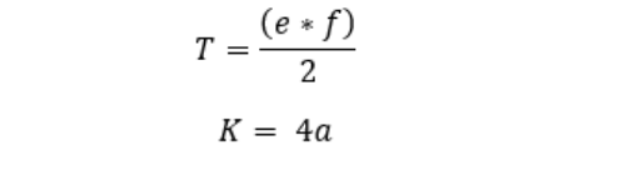
A rombusz fogalma
A rombusz egy olyan négyszög, melynek minden oldala egyenlő hosszúságú. Minden paralelogramma, trapéz, húrtrapéz és deltoid egyben rombusz is.
Tulajdonságai
A rombusz legfontosabb tulajdonságait pontokba szedjük.
- A rombusz átlói merőlegesek egymásra
- A rombusz átlói felezik egymást
- A rombusz szemközti szögei egyenlő nagyságúak
- A rombusz középpontosan és tengelyesen szimmetrikus alakzat
- A rombusz egy oldalon fekvő szögei 180 fokra egészítik ki egymást.
- A középpontja körüli 180 fokos elforgatás saját magába képzi
Minden rombusz középpontosan szimmetrikus – az átlói metszéspontja ez a szimmetria középpont. Minden rombusznak minimum két darab szimmetriatengelye van, ezek az átlói.
A rombusz területe
A rombusz területe több féleképp is meghatározható – akár trigonometikus úton is. Lássuk az ide vonatkozó képleteket!

ahol „a” jelöli a rombusz alapját, „m” pedig annak a magasságát. Egy másik lehetséges meghatározási mód, ha ismerjük a rombusz átlóinak hosszát.
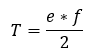
ahol e és f az egymásra merőleges átlókat jelöli. Egy harmadik lehetséges, praktikus számítási mód:

ahol „a” a rombusz oldala, míg a rombusz egyik tetszőleges szöge. Valójában mindegy, hogy melyik, hiszen a kiegészítő szögek szinusza mindig ugyanakkora.
A rombusz kerülete
A rombusz kerülete annak oldalainak összeadásával számítható ki. Ha a rombusz oldala „a” hosszúságú, akkor a kerülete
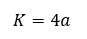
A négyszög szerkesztése
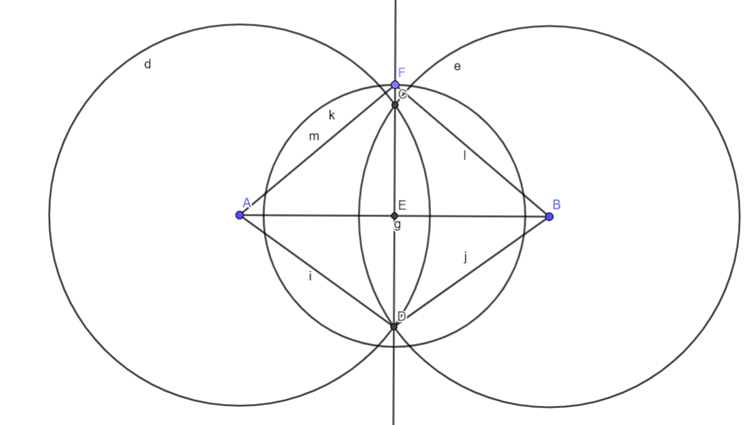
Hogyan kell egy rombuszt megszerkeszteni? Merül fel mindenkiben matematika órán ez a teljesen jogos kérdés. Először vegyünk fel egy tetszőleges szakaszt a síkon – legyen ez a rombusz egyik átlója. Ezt a szakaszt felezzük meg egy szakaszfelező merőlegessel, és a szakaszfelező metszéspontból rajzoljunk egy tetszőleges sugarú kört – annak a függvényében, hogy a másik átlót milyen hosszúra szeretnénk. Ekkor a kör és a szakaszfelező merőleges metszéspontjai adják majd meg a másik két csúcsát a négyszögnek. A szerkesztési ábrát alább tekinthetjük meg.
A rombusszal kapcsolatos legfontosabb képletek
|
Terület (átlókkal számolva) |
|
|
Terület (oldalakkal és szögekkel számolva) |
|
|
Kerület |
|
|
Átló (egyik) |
|
|
Átló (másik) |
|
|
Beírt kör sugara |
|
Ismétlő kérdések
Íme, lássunk néhány ismétlő tesztkérdést, hogy láthassuk: valóban tisztában vagyunk-e a rombuszhoz kapcsolódó állításokkal.
I. feladat
Döntsük el, hogy mely állítások igazak az alábbiak közül a rombuszokra!
A,
Minden rombusz tengelyesen szimmetrikus.
B,
Minden rombusz deltoid is egyben.
C,
Minden rombusz téglalap is egyben.
Megoldás.
Az (A) állítás igaz, hiszen a rombusz átlója mindig szimmetria tengelye a rombusznak. A (B) állítás is igaz, hiszen a rombusz egy olyan deltoid, melynek oldalai egyenlő hosszúak. Azonban a (C) állítás nem igaz, hiszen nem minden rombusz téglalap.
II. feladat
Egy rombusz átlóinak hossza 9 és 5 centiméter. Számítsuk ki a területét és a kerületét.
Megoldás.
A területét nagyon könnyű kiszámolni, hiszen ismert a képlet, ami a rombusz átlói, és annak a területe között teremt egy összefüggést:
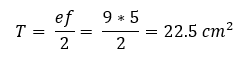
A kerületét úgy tudjuk meghatározni, hogy kiszámítjuk az oldal hosszúságot. Mivel a rombusz átlói merőlegesek egymásra, ezért könnyedén használhatjuk a Pitagorasz-tételt. Jelöljük a rombusz oldalát „a”-val, ekkor fennáll az alábbi összefüggés:

Összefoglalás
A rombusz esszenciális része már az általános iskolai tananyagnak is. Akár középiskolai felvételiről lenne szó, akár érettségiről, vagy a következő matematika témazáróról – mindenképp érdemes tisztában lenni a rombusz fogalmával, tulajdonságaival, hiszen rengeteg olyan feladat kerülhet elő, ami kapcsolódik a rombuszokhoz. Hogyan kell a rombusz területét és kerületét kiszámolni? Mik a rombusz tulajdonságai? Hogyan kell egy rombuszt megszerkeszteni? Ezekkel a kérdésekkel érdemes tisztában lenni.