VAGY

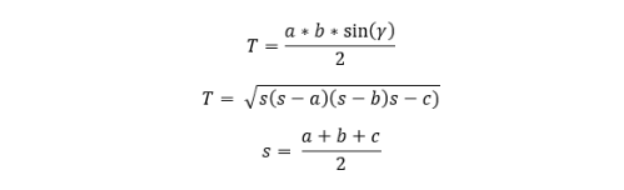
A háromszög fogalma
A háromszög egy olyan geometriai alakzat, melynek három oldala, és három csúcsa van. Egy háromszög lehet általános háromszög, vagy pedig – a speciális eseteket vizsgálva – derékszögű, egyenlő oldalú vagy egyenlő szárú háromszög. Amennyiben a háromszög speciális, általában van egyszerűbb mód a kerület-és terület számolásra.
Az általános háromszög területe és kerülete
Az általános háromszög területének és kerületének meghatározásával kezdjük, utána fogunk haladni a specifikusabb esetek felé. Érdemes megjegyezni, hogy ezek a képletek minden egyes háromszögre ugyanúgy alkalmazhatók, és érvényesek.
Egy tetszőleges háromszög területe megadható úgy, hogy az egyik tetszőleges oldalának hosszát összeszorozzuk az adott oldalhoz tartozó magassággal, és a kapott eredményt osztjuk kettővel.
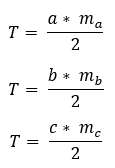
Egy általános háromszög területe szintén kiszámítható a Hérón-képlettel.

Ebben a képletben s a háromszög félkerületét jelöli, mely képlettel így fest:

A koordinátarendszer fogalmát már lehet, hogy tanultad. Ez esetben azt is megteheted, hogy a háromszöget berakod egy derékszögű koordináta-rendszerbe. Jelölje a háromszög csúcspontjait a számpárok. A háromszög területszámítása az alábbi képlettel lehetséges:
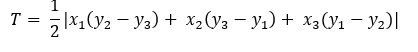
Természetesen megadhatjuk az általános háromszög területét a beírt és körülírt körének függvényében. Amennyiben R jelöli a körülírt kör sugarát, r pedig a beírt kör sugarát, az alábbi képletek érvényesek:
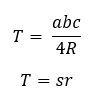
Egy tetszőleges háromszög területe kiszámítható trigonometrikus úton is. Nincs más dolgunk, mint hogy két tetszőleges szomszédos oldal hosszát összeszorozzuk a bezárt szögük szinuszával. Az alábbi képletek használhatók és érvényesek:

Az általános háromszög kerülete egyszerűen úgy adható meg, hogy összeadjuk a határoló oldalak hosszát.

A derékszögű háromszög területe és kerülete
Egy derékszögű háromszög területét megadhatjuk úgy, hogy a két egymásra merőleges oldalát (befogóit) összeszorozzuk, és az eredményt kettővel elosztjuk. A helyes képet:
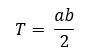
Egy derékszögű háromszög kerületének kiszámításakor használjuk ki azt a tényt, hogy az átfogó hossza megadható a befogók hosszának függvényében.
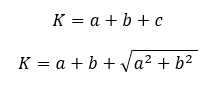

Az egyenlő szárú háromszög területe és kerülete kiszámítása
Egy egyenlőszárú háromszög szárainak közös végpontjából az alapra állított merőleges szakasz felezi a háromszög alapját. A magasság tehát viszonylag könnyen megadható az alap és a szárak függvényében, írjuk fel Pitagorasz tételét!

vagyis

A háromszög területe tehát

Az egyenlő szárú háromszög kerülete úgy adható meg, hogy összeadjuk az oldalait. Mivel két oldala egyenlő hosszúságú, ezért a helyes képlet:

A szabályos háromszög területe és kerülete
A szabályos háromszög területe négyzetesen arányos az oldal hosszal. A képlet az alábbi:

A kerületszámításkor használjuk ki azt a tényt, hogy az oldalak hossza egyenlő!




